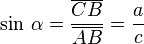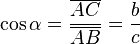origen de los signos matematicos

 El matemático alemán Michael Stifel (1485 -1567) en su obra Arithmetica Integra popularizó los símbolos “+” y “-” desplazando a los signos “p” (plus) y “m” (minus). Según el matemático español Rey Pastor (1888-1962), los signos “+” y “-” fueron utilizados por primera vez por el científico alemán Widmann (1460-1498). Robert Recode (1510-1558), matemático y médico inglés, fue el creador del símbolo “=“. Para él no había dos cosas más iguales que dos lineas rectas paralelas. 

- El símbolo que conocemos como “raíz de” apareció por primera vez en un libro alemán de álgebra de 1525. Antes, para designar la raíz de un número se escribía literalmente “raíz de …”. Para abreviar se usó simplemente la letra “r“, pero cuando los números eran grandes se alargaba el trazo horizontal de la misma dando origen al símbolo que utilizamos hoy en día. 

- El matemático François Viète (1540 – 1603) fue el primero en utilizar letras para designar las incógnitas y constantes. 

- A Tomas Harriot (1560 – 1621) le debemos los signos actuales de “>” y “<“, y el “.” como símbolo de multiplicación. 

- Los símbolos de multiplicación “x” y división “:” fueron introducidos por el matemático William Oughtred (1574-1660) en el año 1657. 

- El símbolo de la integral fue propuesto por Gottfried Leibniz (1646-1716) y lo extrajo de la palabra latina “summa” tomando su inicial. A Leibniz le debemos muchos más signos notacionales como “dx” y además fue quien popularizó el “.” como signo de multiplicación. 

Razones trigonométricas

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo , correspondiente al vértice A, situado en el centro de la circunferencia.

• El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.

• El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

• La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

Representación gráfica

Representación de las funciones trigonométricas en el plano cartesiano (x,y), los valores en el eje x expresados en radianes.

Física matemática

La física matemática es el campo científico que se ocupa de la interfaz entre las matemática y la física. El Journal of Mathematical Physics la define como «la aplicación de las matemáticas a problemas del ámbito de la física y el desarrollo de métodos matemáticos apropiados para estos usos y para el desarrollo de conocimientos físicos.»,¹ la teoría de la elasticidad, la acústica, la termodinámica, la electricidad, el magnetismo y la aerodinámica


En muchos de esos campos los físicos matemáticos han desarrollado teoremas y han demostrado propiedades generales a los que conducen determinadas teorías que han servido para reformular los modelos físicos. En física matemática, los métodos de trabajo están en general más cerca del método deductivo usado en matemáticas que de los métodos inductivos más típicos de la física experimental. A veces el uso del término «física matemática» es idiosincrásico. Mientras que ciertas partes de la matemática que inicialmente se desarrollaron a partir de la física no son consideradas elementos de la física matemática, algunos otros campos estrechamente vinculados sí lo son. Por ejemplo, las ecuaciones diferenciales ordinarias y la geometría simpléctica son generalmente consideradas disciplinas puramente matemáticas, mientras que los sistemas dinámicos y la mecánica hamiltoniana sí pertenecen a la física matemática.

Matemática en la vida cotidiana

#1: Programación

Tener un blog personal o una página web es muy habitual hoy en día. Existen muchas plataformas como WordPress o Blogger que hacen que esto posible sin tener conocimiento de lenguajes de programación. Sin embargo, si quieres optimizar tu sitio web, más te vale tener nociones matemáticas para calcular cómo distribuyes el espacio y las dimensiones de tus recursos visuales.

#2: Operaciones Bancarias

Hipotecas, planes de pensiones, préstamos, comisiones, inversiones… todo tipo de acuerdo que tengas con un banco estará gobernado por las matemáticas. Cuanto más sepas, más probabilidades tendrás de hacer lo correcto con tu dinero. Además, si te gusta viajar e ir a otros países o incluso comprar online, te enfrentarás a cambios de moneda en múltiples ocasiones.

#3: Probabilidades

La estadística suele ser una de las ramas de las matemáticas más usadas. Todos calculamos probabilidades en nuestra vida cotidiana. Probabilidades de ser admitidos en la universidad, de acertar, de ganar la lotería, etc. Además, si te gusta jugar al póker, a la ruleta o a otros juegos de azar, ¡más te vale saber algo de estadística

#4: Diseño de escenarios

La estadística juega un papel fundamental al analizar resultados pasados pero, sobre todo, para diseñar escenarios de futuro. Las previsiones optimistas, realistas y pesimistas son habituales en todo tipo de negocios y proyectos. Para construirlas, la progresión matemática es el elemento principal.

#5: Música

¿Sueñas con ser un músico conocido? Quizás te interese saber que algunos de los músicos más famosos de todos los tiempos, como Mozart o Bach, utilizaron elementos matemáticos en sus obras, relacionando algunos de sus compases con la razón áurea. Más adelante, Joseph Schillinguer, detalló un sistema de composición basado en principios matemáticos, principalmente la geometría. Esto demuestra la conexión entre música y matemáticas.

Hola, hoy buscando nuevas cosas para el blog encontré una página que muestra 10 curiosidades de matemática. Les dejo las 5 que más me gustaron. 



Curiosidades de Matemática.

1. Lleva goma de mascar a tu próximo examen de matemáticas

Según se ha observado globalmente, aquellos estudiantes que durante una prueba o un examen de matemáticas mastican goma de mascar son los que consiguen mejores calificaciones. Así lo determinó un largo estudio desarrollado por un grupo de investigadores de la Louisiana State University.

2. Pizza

Si tienes una pizza con un radio Z y una altura A, su volumen será: PI*Z*Z*A.

3. ¿Cómo atar un lazo?

Según los matemáticos, existe un total de 177.147 formas distintas de atar un lazo.

4. La paradoja del regalo de cumpleaños

En matemáticas existe una paradoja muy curiosa llamada “la paradoja del regalo de cumpleaños”. Esta dice que en una fiesta de cumpleaños con 23 invitados, hay un 50% de probabilidades de que al menos 2 personas lleguen con el mismo regalo.

5. Muchísimo conocimiento en matemáticas

Para el año 1900, todo el conocimiento científico de la humanidad podía guardarse en un total de 80 libros. Hoy en día, las matemáticas se han desarrollado mucho más y con los nuevos aportes, se necesitarían 100.000 libros para la misma tarea. 

Les dejo el link para que vean los otros 5, saludos.  

http://www.batanga.com/curiosidades/5896/conocias-estos-10-curiosos-hechos-sobre-las-matematicas

 DIAGRAMA DE ÁRBOL

Un diagrama de árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio. En el cálculo de la probabilidad se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de árbol.

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

¿Porqué estudiamos matemáticas?   

Permanentemente se escucha decir a muchos alumnos frases como ''Para que estudio matemática'', ''Esto no me sirve para nada en la vida'' y acá les dejo razones por las cuales se estudia la matemática.

1. Estudia matemáticas para reforzar tu inteligencia.

2. Estudia matemáticas para ganar más dinero.

3. Estudia matemáticas para perder menos dinero.

4. Estudia matemáticas para ahorrar tiempo.

5. Estudia matemáticas porque vives en un mundo globalizado.

6. Estudia matemáticas porque vas a vivir en un mundo de constantes cambios.

7. Estudia matemáticas porque no te cerrará ninguna puerta.

8. Estudia matemáticas porque es interesante en sí misma.

9. Estudia matemáticas porque en el futuro te la vas a tener que enfrentar más y más seguido.

10. Estudia matemáticas para trascender, no solo en el colegio.

11. Estudia matemáticas porque las matemáticas son creativas.

12. Estudia matemáticas porque es cool.

Me resultó interesante el artículo ya que usualmente las matemáticas son el “cuco” de muchos estudiantes, que incluso terminan siendo un factor determinante para escoger otras carreras en las que se imaginan que las matemáticas presentes en menor medida. Pero como dice el artículo, las matemáticas están en todos lados, en todas las disciplinas, y tarde o temprano nos las vamos a encontrar en distintos ámbitos de nuestras vidas.

Teniendo los profesores o maestros con la capacidad de trasmitir el por qué de estudiar matemáticas desde etapas tempranas de nuestras vidas quizás nos permitirían (y permitan a futuras generaciones) comprender mejor las matemáticas y de una forma entretenida.

¡Espero que les halla gustado!