Expresiones algebraicas

Trabajar en álgebra consiste en manejar relaciones numéricas en 

las que una o más cantidades son desconocidas. Estas cantidades se 

llaman variables,incognitas o indeterminadas y se representan por 

letras.

Una expresión algebraica es una combinación de letras y números 

ligadas por los signos de las operaciones: adición, sustracción, 

multiplicación, división y potenciación. 

Ejemplo: x.2

Clasificación de las expresiones algebraicas

Monomio

Un monomio es una expresión algebraica en la que las únicas

operaciones que aparecen entre las variables son el producto y la

potencia de exponente natural.

Binomio

Un binomio es una expresión algebraica formada por dos monomios.

Trinomio

Un trinomio es una expresión algebraica formada por tres

monomios.

Polinomio

Un polinomio es una expresión algebraica formada por más de tres monomios

Partes :

El coeficiente del monomio es el número que aparece multiplicando a 

las variables.3

Parte literal

La parte literal está constituida por las letras y sus exponentes.

Grado

El grado de un monomio es la suma de todos los exponentes de las 

letras o variables.

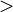
Inecuación

En matemáticas, una inecuacion es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad.^1 2 Si la desigualdad es del tipo  o  se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥ se denomina inecuación en sentido amplio.³

Del mismo modo en que se hace la diferencia de igualdad y ecuación, una inecuación que es válida para todas las variables se llama inecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.⁴ Los valores que verifican la desigualdad, son sussoluciones.

• Ejemplo de inecuación incondicional: .
• Ejemplo de inecuación condicional: .

Clasificación

Los criterios más comunes de clasificación del ejemplo: .

• • De dos incógnitas. Ejemplo: .
  • De tres incógnitas. Ejemplo: .
  • etc.

• Según la potencia de la incógnita,
  • De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo: .
  • De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo: .
  • De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo: .
  • etc.

Nota: estas clasificaciones no son mutuamente excluyentes, como se muestra en el último ejemplo.

¡Para las profes! Leanlo, muy bueno. 

         

    7 razones para usar la calculadora en clase.

Las calculadoras son herramientas cada vez más imprescindibles, aparatos simples y eficaces con los que se pueden resolver las operaciones más complejas. ¿Pero son realmente tantas las ventajas que pueden aportar a la enseñanza? Nosotros te traemos hasta 7 razones que lo confirman:

1. Ahorra tiempo: Cuando el objetivo es desarrollar capacidades generales de razonamiento matemático o la investigación de pautas numéricas, la calculadora es necesaria para evitar gastar los minutos resolviendo largas y tediosas operaciones. ¡Investigar es también una parte vital del conocimiento que a veces dejamos de lado por falta de tiempo!
2. Es necesario aprender su uso: Tanto en secundaria como en Bachillerato, o incluso en la Universidad, la calculadora se convierte en un bien necesario inevitablemente; por lo que los estudiantes la usarán cada vez con más frecuencia. Y ya que se trata de un instrumento cotidiano, ¿quién mejor que los docentes para enseñarles a manejarlas correctamente?
3. Son neutrales ante los fallos: Los errores no son percibidos por el estudiante como una reprobación o crítica, ya que es él mismo el que corrige sus ejercicios. Una genial manera para potenciar la capacidad de autocrítica y de gestión de los problemas.
4. Contribuyen a motivar al alumnado: Los cálculos reiterativos reducen considerablemente el interés por las matemáticas. Los estudiantes tienden a aburrirse cuando las clases se basan en resolver monótonamente hojas y hojas plagadas de ejercicios. ¿Y si hacemos alguna actividad diferente con la calculadora como protagonista?
5. Fomentan el espíritu crítico: Cuando se prohíbe o se reduce el uso de las calculadoras, éstas se convierten en herramientas anheladas y admiradas por los alumnos, que acabarán por considerarlas la mejor forma de resolver un cálculo. Sin embargo, su uso cotidiano puede hacer que los estudiantes duden y se posicionen de forma crítica ante ellas. ‘¿Habré tecleado bien las cifras?’, pensarán.
6. Ayudan a detectar posibles errores: La posibilidad de verificar los cálculos rápidamente posibilita a los estudiantes pedir ayuda inmediata a las respuestas erróneas y a detectar posibles equivocaciones.
7. Permiten sacar el lado más divertido de las matemáticas: Además de aprovechar la inmensa capacidad de atracción que tienen en los más jóvenes las pantallas y las nuevas tecnologías, también podemos utilizar las calculadoras para hacer algo más original en nuestras clases. ¡Echa un vistazo a estos juegos pensados específicamente para esta herramienta!

Pi

3,1415926535897932384… Se trata del número Pi, una cifra infinita que indica la constante proporción de una circunferencia con su diámetro. Se reduce a 3,14 en su expresión más simple, y se representa con la letra griega π. Fue en 2009 cuando la Cámara de Representantes de los Estados Unidos declaró la celebración del Día de Pi el 14 de marzo, después de que el físico Larry Shaw lo propusiera y fuera ganando popularidad.

El número Pi es una de las constantes matemáticas más importantes, y también es vital en otras ciencias y áreas del conocimiento. Muchos proyectos no se podrían llevar a cabo, o sería muy difícil, sin el número Pi (como la arquitectura, ingenierías o mecánica), ya que sirve para calcular diferentes longitudes y espacios.  Por ello, no hay mejor ocasión que este día para realizar una jornada centrada en las matemáticas, ¿no te parece?

A continuación, te proponemos 5 actividades que puedes realizar con motivo de esta celebración el próximo día 14, y que conseguirán que los estudiantes descubran esta cifra matemática de una forma muy diferente. ¡Toma nota!

1. ¿Cuál es la historia del número Pi?: En esta unidad didáctica, conoceremos las diferentes aproximaciones a esta constante que se han dado a lo largo de la Historia, centrándose en el método de Arquímedes. Una apasionante forma de descubrir que el conocimiento se ha ido creando con el paso de los siglos, y cómo éste ha ido evolucionando.
2. Trabajando con el área del círculo: Un documento con diferentes formas y ejercicios de calcular la superficie de la circunferencia, enseñando a los estudiantes el porqué de la fórmula matemática que se utiliza y a comprender el concepto de ‘infinito’.
3. ¡El número Pi nos rodea!: Una interesante experiencia puede consistir en seleccionar varios objetos de diversos tamaños (bote de cristal, pelota, celo, chincheta…) y medir el diámetro y longitud de su circunferencia para hallar nuestras propias aproximaciones al número Pi. Diseñar unos carteles donde se relacione esta constante matemática con los diferentes objetos del entorno puede ser una excelente manera de concluir esta actividad.
4. Algunos ejercicios prácticos: Un generador de ejercicios que crea problemas para calcular el radio, el diámetro, la circunferencia o el área de un círculo, cuando se da el valor de uno de ellos. Además, permite incluir imágenes circulares en ellos, y modificar el estilo y tamaño de las letras. Todos los ejercicios vienen con respuestas.
5. El invariable número Pi: Se trata de una actividad interactiva con la que podrás experimentar con diferentes ejemplos como esta constante matemática es siempre la misma, sin importar las medidas de los círculos con los que trabajemos